•
April 13, 2025
Yan, S. (2016, March 3).
The human brain, in all its complexity, can hold thoughts, emotions, and perceptions of the observable. However, these ideas are constantly shifting, sculpted by personal experience and time. This gives rise to a diverse spectrum of memories, ranging from core memories like the smiles of our loved ones to momentary ones like the most recent song you listened to. These memories influence how we think and act, continuously adapting as we gain new information from interacting with the world.
Surprisingly, we can quantify this dynamic behavior through a machine learning model: The Long Term Short Term Neural Network (LSTM). Like our minds, which hold onto the significant and let go of the fading, the model mimics this ability by retaining long-term information, forgetting unnecessary noise, and updating short-term perceptions.
Let’s Talk Theory:
Throughout this article, I will be using terminology like weights and biases. Weight is a number you multiply by an input number, and bias is a number you add to an input number.
Here is a quick example:

So let’s imagine that at a specific point, the value is 5. This means the input is 5. If it goes through a weight of 2, it will multiply with the weight value and now be 10. Then, if there is a bias of 4 applied, then the new stored value of 14. It is just multiplication and addition!
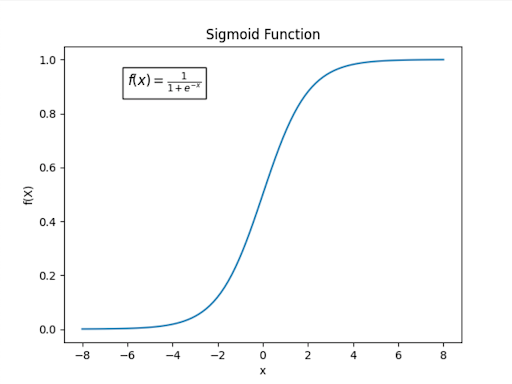
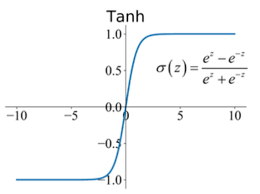
Long-Term Short-Term Neural Networks utilize two fundamental mathematical concepts: the sigmoid activation function and the tanh activation function. The sigmoid activation function converts any x value (the input) into an output from 0 to 1. On the other hand, the tanh converts any x-value (the input) into an output from -1 to 1.
Sigmoid Graph:
Code Academy. (2023, July 7).
Tanh Graph:
Papers with Code. (n.d.).
It's important to note that the Sigmoid Function creates percentages to apply to values. Tanh function, on the other hand, creates new values to be input to pre-existing ones (updating).
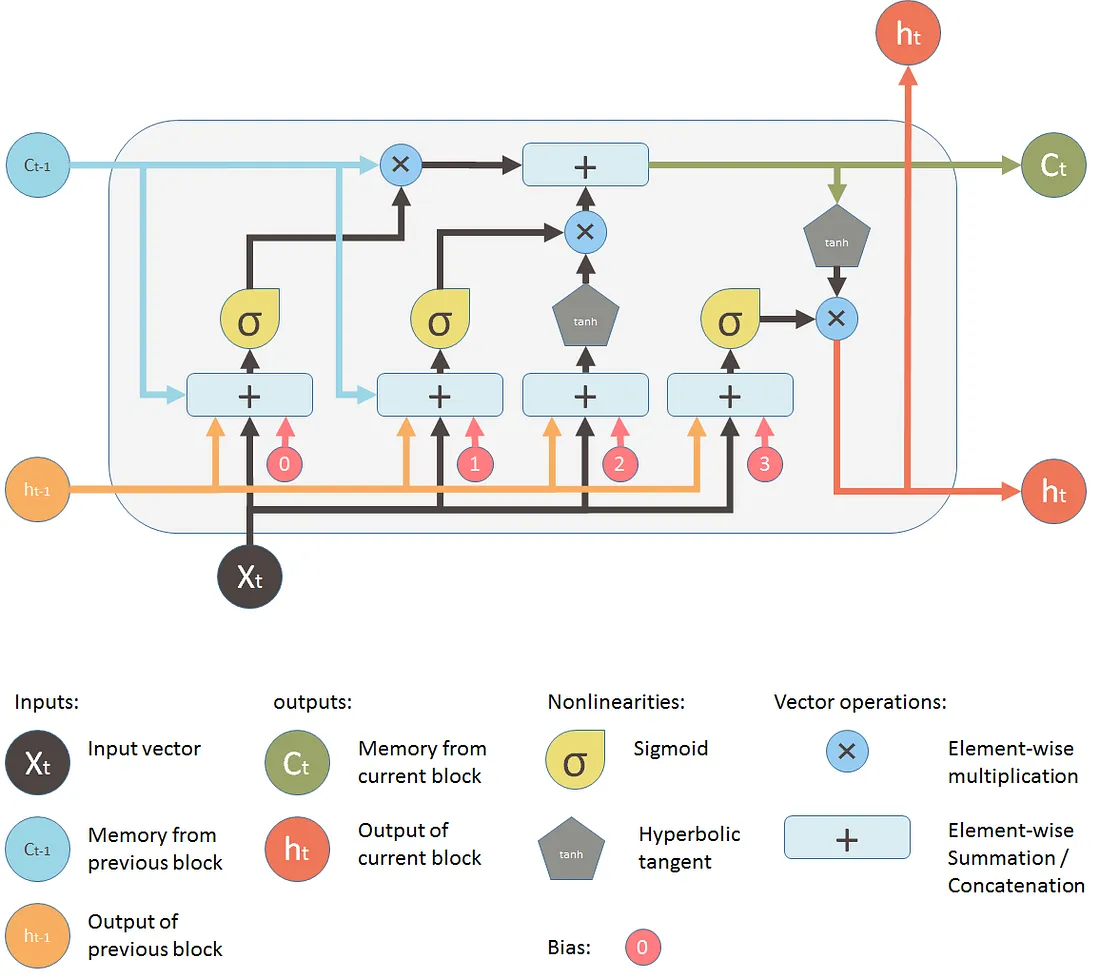
The LSTM is made up of 3 primary “gates” or stages.
-
1. Forget Gate: Percentage of original Long Term Memory Remembered
-
2. Input Gate: Addition of potential Long Term Memory to the original
-
3. Output Gate: Calculate a new Short Term Memory
Long-term memory is the memory that carries knowledge from past experiences that the LSTM decided were important. Think of it as something meaningful that stays with you, such as when you graduated from high school. Short-term memory is the most recent knowledge, such as what you had for breakfast, useful right now but easy to forget.
Input is the new information getting fed into the LSTM. This is like looking at an object or listening to something someone said. The entire purpose of the LSTM is to decide if this input is worth remembering in the short term, storing for the long term, or forgetting completely.
Let's look deep into each LSTM Gate for a better understanding. Let's talk about how it makes those decisions.
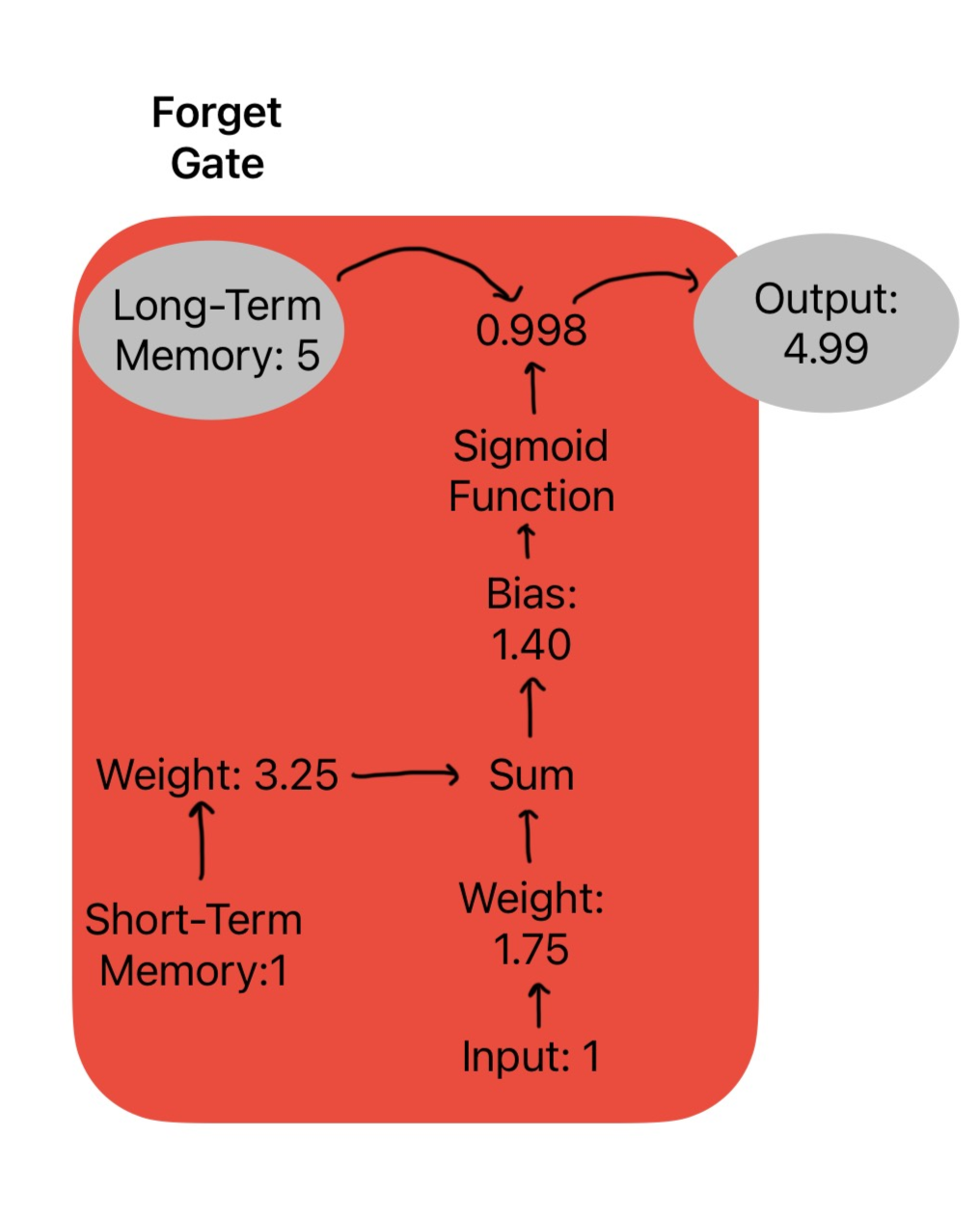
1. Forget Gate: What should we erase from memory?
First, the LSTM takes the current input and the short-term memory. Then it applies unique weights to each value and sums them together. A bias term is added and passed through a sigmoid activation function. The sigmoid outputs a percentage between 0 and 1.
For example, in the diagram below, the input and short-term memory are both 1.
StatQuest with Josh Starmer. (2022, November 6).
We multiply the values with their corresponding weights:
-
Input × 1.75 = 1.75
-
Short-term memory × 3.25 = 3.25
Then we add them together and apply the bias:
-
Total + Bias: (1.75 + 3.25) + 1.40 = 6.40
6.40 is passed into the sigmoid function, which outputs 0.998. This means 99.8% of the long-term memory is kept, giving us a new value of 4.99.
So the forget gate decided, “Yeah, almost all of that memory is still useful.”
2. Input Gate: What new information should we add?
This is the second step of the LSTM formula. This gate does two things: calculate a new memory with the tanh activation function and decide how much of the new memory is added to the long-term memory that was kept after the forget gate. Surprisingly, this gate has two pathways.
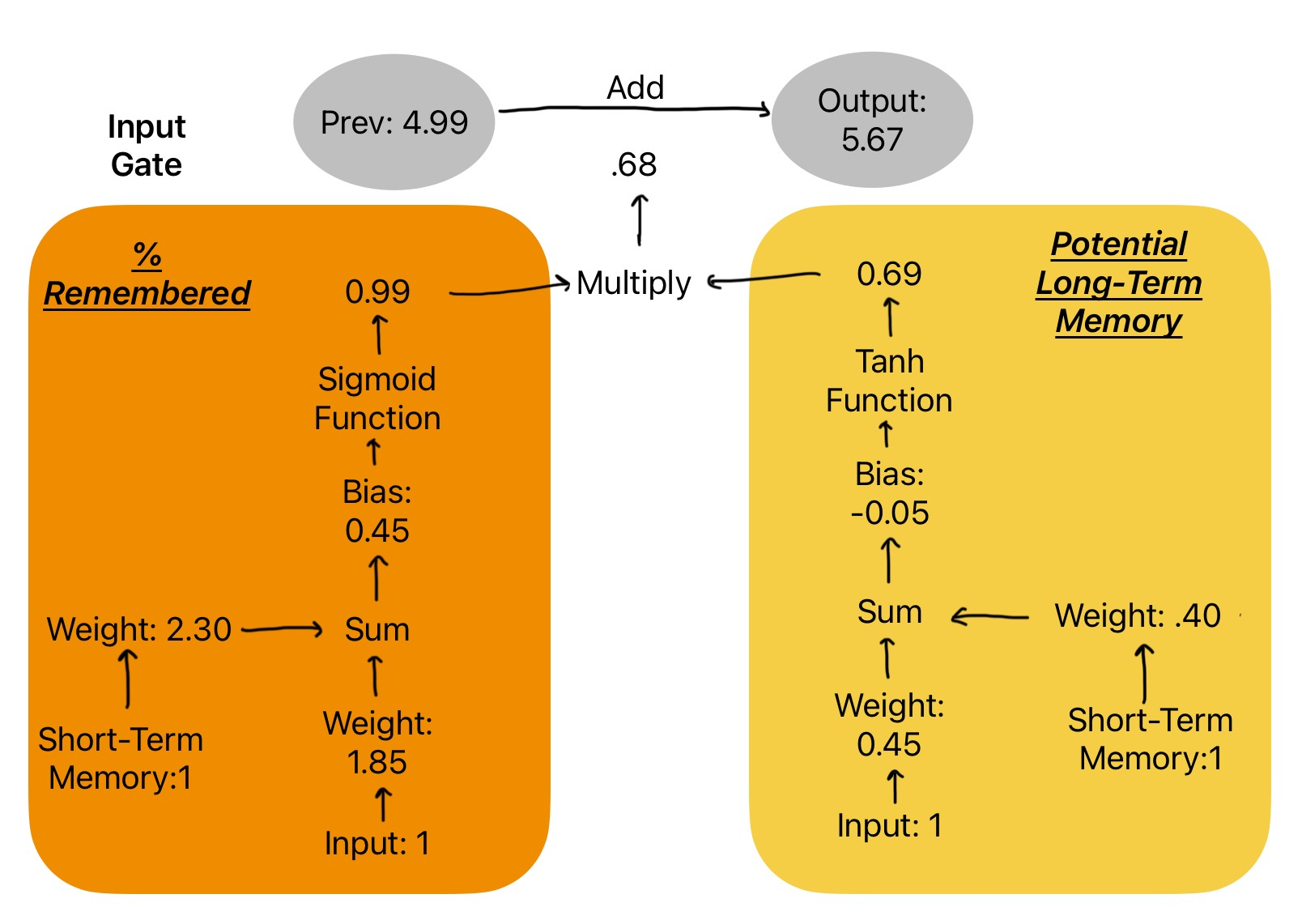
StatQuest with Josh Starmer. (2022, November 6).
Once again, the LSTM takes the current input and the short-term memory for both pathways. Each pathway has its unique weights and biases. However, one goes through a sigmoid activation function and one goes through a tanh activation function. The two outputs are multiplied and added to the previous long-term memory from the forget gate.
In the orange (sigmoid) path:
-
(1 × 2.30) + (1 × 1.85) + 0.45 = 4.60
The sigmoid turns this into 0.99, which means "keep 99% of all the new info."
In the yellow(tanh) path, we calculate: (1 × 0.45) + (1 × 0.35) + (–0.05) = 0.80, which the tanh function gives about 0.69.
Now multiply them:
-
0.99 × 0.69 = 0.68
This value is then added to the long-term memory from the forget gate:
-
4.99 + 0.68 = 5.67
So, the input gate decided “this new info is valuable,” and the memory is updated again. This new long-term memory holds context across time and will pass it down to the next LSTM unit (starting the process all over again).
3. Output Gate: Changing the Short-Term Memory
The purpose of this gate is to update the short-term memory.
Just like before, the output gate uses the same two inputs: the current input and the short-term memory from the previous step. But this time, there’s only one path. Specific weights and a bias are applied to these values, and the result is passed through a sigmoid activation function.
At the same time, the newly updated long-term memory (from the previous gates) is passed through a tanh function to squash it into a manageable range.
Finally, the outputs of the sigmoid and tanh are multiplied together to produce the new short-term memory for this time step.
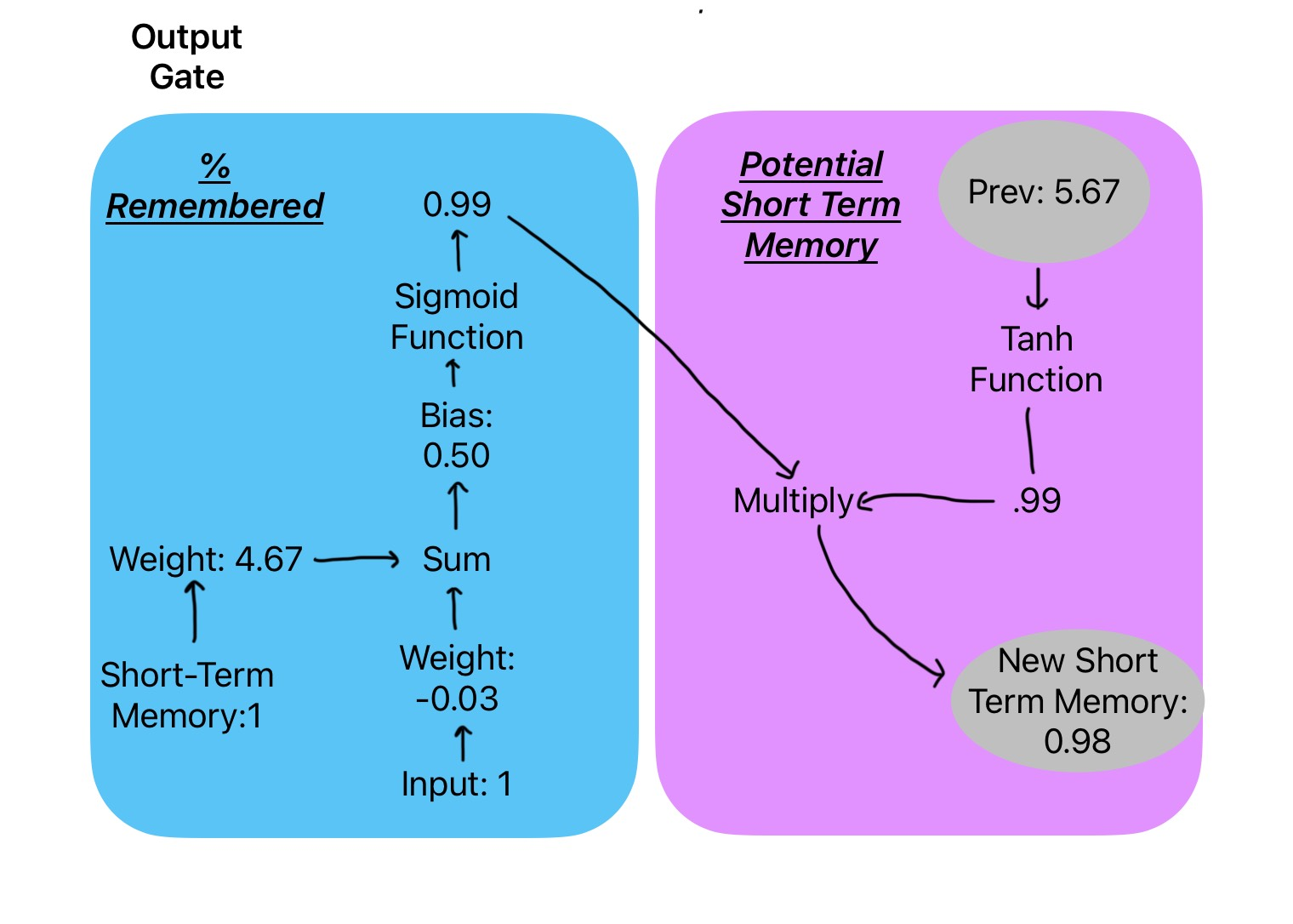
StatQuest with Josh Starmer. (2022, November 6).
In the diagram below, the input and short-term memory are both 1. Each gets its own weight.
We multiply:
-
Input × (-0.03) = -0.03
-
Short-term memory × 4.67 = 4.67
Then we add them together and apply the bias:
-
(4.67 + (–0.03)) + 0.50 = 5.14
That number is passed into the sigmoid activation function, which outputs 0.99. This means 99% of the current memory is allowed to pass through.
At the same time, the new long-term memory is passed into a tanh function, which also gives 0.99.
Finally, we multiply:
0.99 × 0.99 = 0.98
This gives us the new short-term memory: 0.98.
Once the LSTM finishes updating its short-term memory through the forget, input, and output gates, that short-term memory becomes the key to making a prediction. Even if you’re working with just one time point, the LSTM processes that input and forms a kind of “thought,” a numerical summary of what it understood. This summary is called the short-term memory, or hidden state. To turn that into a prediction, we pass it into a Dense layer, which is just a simple layer that applies its own weights and biases. The Dense layer takes the LSTM’s current “thought” and converts it into a final number, which is your prediction for the next time step. For example, if the hidden state was 0.98, the Dense layer might multiply it by 2 (the weight), add 1 (the bias), and predict 2.96 as the next value. That is how the memory updates we’ve been walking through actually lead to real, useful predictions.
References:
-
1. Code Academy (2023, July 7). Sigmoid Activation Function. https://www.codecademy.com/resources/docs/ai/neural-networks/sigmoid-activation-function
-
2. StatQuest with Josh Starmer. (2022, Nov. 6). Long Short-Term Memory (LSTM), Clearly Explained [Video]. YouTube. https://www.youtube.com/watch?v=YCzL96nL7j0
-
3. Yan S. (2016, Mar. 3). Understanding LSTM and its diagrams. Medium. https://blog.mlreview.com/understanding-lstm-and-its-diagrams-37e2f46f1714
-
4. Tanh Activation. https://paperswithcode.com/method/tanh-activation

